别迷信：钱学森数学厉害吗？不！一点都不厉害！就是一般水平！

实话实说，人得有清醒的自我认知，要不然会飘。这是今天讨论问题的前提。

W君一直觉得头条这边的粉丝关心的话题是军事、国际形势以及生活中的那些屎尿屁。前阵子头条的认证规则变了，W君从军事领域转到科学领域，最近写文章也就尽量脱离开一些军事内容，想给大家讲讲批在军事外衣下的科技和狠活。但始料不及的是最近发现一篇讲数学的文章大家的回复和关注度超级高。甚至有人这样回复，已经开始让W君推荐数学的入门书了。

第一、真心高兴，大家能对数学有兴趣；第二、就是有点惭愧了。惭愧就在于W君自己也不是什么数学家，只是日常的工作中经常拿着别人写好的公式当作工具来用罢了。这和建筑工地上的农民工并没有什么分别，只不过他们拿着的是别人发明的铁锹和风镐，而W君用的是别人总结出的公式。

恰巧，最近关于钱老的一个言论又成了新闻热点，钱老说“人再笨，还能学不会微积分吗？”

有人就回复“钱老还是被保护的太好了，很少接触我们这些没进化完全的猴子”。

其实，如果你在工作中经常用到数学，你会觉得钱老这句话一点都不为过。

展开全文

这句话相当于成吉思汗讨论骑马射箭，他也会说“人再笨还能学不会骑射吗？”，放在一般的草原牧民的视角这句话一点毛病都没有，就是完全绝对正确的。但放在当时中原农耕百姓的眼里大多数人别说骑马射箭，敢骑牛而不摔下来的都是少数。

在骑射这件事上，草原人与中原人的差距并不是天生的，而是环境与文化使然。草原上的孩子从小就跟着父辈骑马放牧，日常饮食、生计乃至荣誉都与骑射紧密相连，它几乎是生存的“常识”。而中原农耕社会以土地为中心，牛是耕地的工具而非坐骑，百姓从小缺乏接触骑马的机会，更别说边骑边射了。草原人视之为日用之学，中原人则觉得是危险的专门技能。

换句话说，中原汉人骑马不行，原因在于摔下马的次数太少，而一个草原牧民小孩成年前摔下马的次数恐怕要比中原一个村子的人落马的总数还要多。

所以，如果成吉思汗当年和治下的中原人说14岁就应该学会骑马，那么中原百姓大抵会这样回复“大汗自幼驰骋于马上，弓矢如臂使指，自是天经地义之事。然我等农家子，生来伏牛执犁，能不被牛角顶翻已属侥幸。大汗言人人可习骑射，此诚至理，然于吾辈，犹若未脱毛之猿猴，未尝进化，岂敢与大草原子弟同日而语。”

这和今天许多人看待微积分如出一辙：对科研工作者而言，它不过是日常工具；可在缺乏数学语境的教育环境里，微积分就像骑射之于中原人，看似高不可攀，实则只是环境不同所造成的隔阂。

老实讲，大多数普通人的生活里，数学毛用没有。买菜靠四则运算，做账靠Excel，手机上自带计算器，算法的逻辑也被APP封装得干干净净。换句话说，哪怕你一辈子不懂微积分只懂得算术也没问题，该吃吃、该喝喝，人生一样能过下去。

正因如此，很多人一听“微积分”就条件反射：这玩意儿跟我八竿子打不着。而再把视角转回钱学森，你会发现他在科学界的“牛逼”，其实并不是像爱因斯坦那样提出震惊世界的理论，而是站在一个需要工程落地的体系里，把微积分、控制论、空气动力学这些现成的工具用得很熟练。

毕竟，钱老在1934年毕业于交通大学、后赴美在麻省理工大学、加州理工学院深造，从1936年开始师从航天泰斗冯·卡门，在1939年，获得加州理工学院航空学和数学博士学位。这里有一个咱们国内很多自媒体没弄明白的事情，很多人认为钱老在1939年6月9日同时获得了了航空学博士和数学博士两个学位，其实钱老所获得的学位是一个工学博士（Doctor of Philosophyin aeronautics and mathematics）其中航空学和数学是并列在一起的。

这个学科是一个结合了航空航天工程和数学领域的专业博士学位，通常专注于航空航天领域的研究和高级问题解决。主要是学会利用数学建模和分析来应对空气动力学、推进和航空航天结构等领域的各种挑战和问题。

不过钱老的这个博士证书的含金量就比普通的博士证书高多了，注意Doctor of Philosophy下的一行小字“Magna Cum Laude（拉丁文：极优等成绩）”。这个位置一般会有四个情况，不标记、“Cum Laude”优等成绩、“Magna Cum Laude”极优等成绩和“Summa Cum Laude”最优等成绩。不过W君查过加州理工学院的记录的，至今“最优等”这个荣誉还没有发出来过。即便是Magna Cum Laude也是凤毛麟角——这才是钱老在加州理工拿博士学位最值得夸耀的地方。以至于后期钱老和冯·卡门搞出来的钱·卡门定律（rule），到现在还在NASA的各种计算和验证中不停的在使用，且没有更好的替代。

不过，就数学本身而言，钱老就是一般水平了。这并不是贬低钱老的成就，而是一个实事求是的事情。你要理解一个很重要的个事情——贝多芬是伟大的钢琴家，但不一定会造钢琴。也像我们一样，我们都会用电脑，但不一定都会造电脑，所以，我们都是“计算机用户”。钱老实际上是一名“数学用户”，数学在他的工作中就是一个已经被熟练使用的工具，骑马射箭而已。在数学领域上并没有钱学森定理和钱学森猜想，甚至可以毫不客气的说，钱学森在数学上的建树为零。当然了，这并不妨碍他的工程学地位也并不妨碍他的《工程控制论》成为封神之作。

所以说，在钱老谈微积分的时候，我们大多少人真的没必要妄自菲薄菲薄把自己比成猴子。

其实前面铺垫这么多，咱还没进入正题呢，就是为了勾起大家的好奇心，让大家对后面的内容哪怕感一点兴趣，W君也就觉得写了2000多个字的铺垫值得了。

钱老说“人再笨，还能学不会微积分吗？”这话W君是同意的，今天也想用后面的一两千字给大家聊聊怎么入门微积分——好了，正片开启：

一、极限：

微积分的门槛，叫“极限”。听着高大上，其实它回答的问题特别朴素：一个东西越来越接近某个点时，它到底会靠到哪儿去？

打个比方，你端着一杯热水放在桌子上，温度会从 90℃ 慢慢降到室温 25℃。你可以问：这水最后会变成几度？答案显然是 25℃。这就是一个“极限问题”：时间无限延长，水温无限接近 25℃，这 25℃就是它的极限。

再换个更形象的例子：想象你追一只小猫，每次快追上时它又往前蹦一小步。你可能永远追不上，但你们之间的距离会越来越小——小到最后无限接近 0。虽然“0”这个瞬间在现实里可能永远不会发生，但数学告诉你：它就是这个过程的极限。

所以，极限的精髓就是：看清变化的终点趋势，而不是纠结于过程里的一次次波动。在数学上“极限”的意义在于让“瞬间”和“连续”变得可描述，同时是可以依据极限来定性的。

例如，肉包子是我们常见的食物，如果我们观察馅，当“馅”趋近于没有的时候以及当馅趋近于无穷的时候，我们会发现下面两个极限关系。

但我们还可以扩展更多的观察点，例如形状。这时候我们就会发现下面的公式：

于是，一个简单的“包子”，在不同极限下就能演化出馒头、烙饼、丸子、肉饼、甚至面条。

这其实就是“极限”的精髓：我们不需要一步步去做饭，只要抓住变量的趋势，就能知道最终会得到什么菜。 数学家是用这种思维，把复杂无比的物理过程、经济模型、工程系统变得可以分析和预测。

——看你是不是不太笨？其实理解到这一步，就已经比当年被“极限”吓跑的中学同桌强多了。

二、导数

在数学里，往往会把导数被定义成一个极限。

在微积分里，导数回答的是这样一个问题：某个量在某一瞬间究竟是怎么变化的。你看这张图，蓝色的曲线代表一个过程，它可以是汽车的行驶路程、股票的价格，甚至是你往包子里塞馅的数量。现在我们关心的，是在某个点 x₀，它的变化趋势到底是什么。

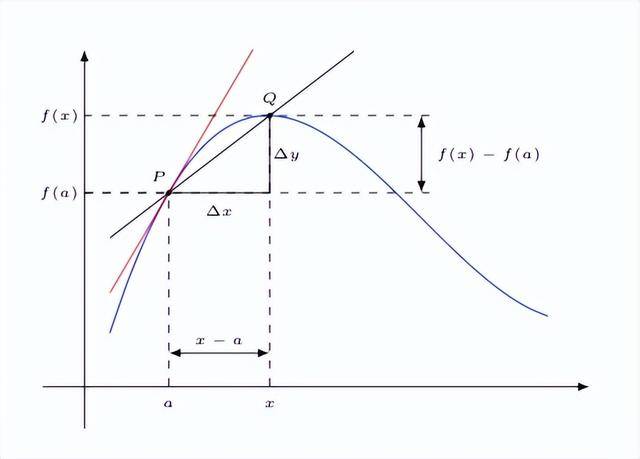
紫色的线段叫“割线”，它连着两个点，表示的是平均变化率。比如说，汽车 1 小时跑了 60 公里，平均速度就是 60 公里每小时。但你真正开车的时候，不可能每一秒都刚好 60，有时候快一点，有时候慢一点。所以，更关键的问题是：在某一瞬间，速度是多少？

这就需要“切线”。红色的直线就是曲线在 x₀ 点的切线，它完美贴合曲线，斜率就是这一瞬间的变化率，也就是导数。数学上写作：

生活里，导数就是车速表上的即时读数，是股价此刻的涨跌，是你手上这勺肉馅落放到包子皮里那一瞬间的“肉量”。它不关心你过去或未来的波动，而是精准刻画“此刻”。

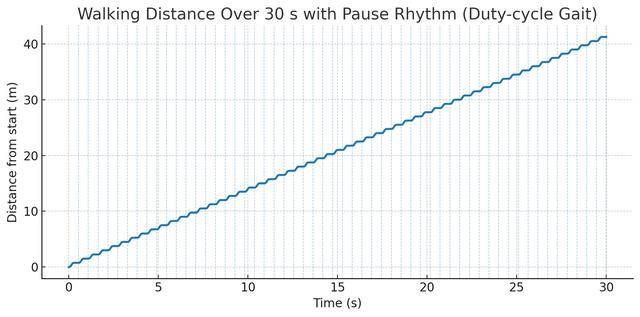
例如人在走路的时候需要抬起左腿、扭胯、放下左腿、抬起右腿、扭胯、放下右腿、再抬起左腿……这样才能向前行走。如果我们考虑人的步幅度停顿那么我们精确的建立时间（横轴）和步幅换算成移动距离（纵轴）的图形就是这样的：

它遵从了下面的公式

单步内速度：

单步累计位移（从该步起点算）：

整段位移s(t)（把前 N 步与当前步相加）：

这样，一来s(t) 就是如果这个人行走t秒后的位移。说白话也就是一段时间内人走出的距离。

如果我们求导数，对 t 求导

最终你会发现

于是你就可以得到了v（速度），那么如果按照v来看这个锯齿形的速度表，你会发现图片就成了这样：

这是啥呢？移动距离=时间 X 速度，速度单位是啥？米/秒！看坐标轴，横轴是秒纵轴是米，很明显速度在这个案例中就是一个斜率。

3、微分

在上一步我们说：速度 v(t) = 位移 s(t) 的导数。换句话说：

这就是微分的原型。

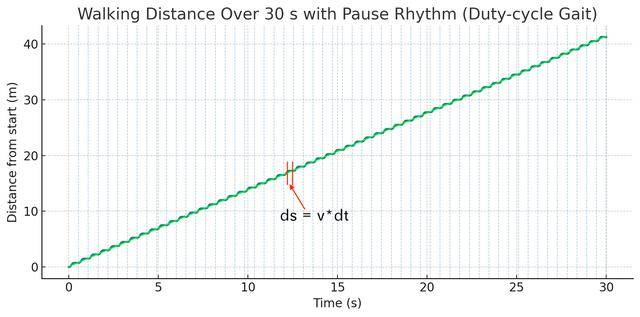
这句话背后的意思特别朴素：人在走路时，30 秒走了 45 米，你算出来的平均速度是 1.5 米每秒。但现实里你哪有“平均速度”这个东西？脚刚抬起来那一瞬间速度几乎是 0，迈出去一半时速度达到最大，落地的时候又慢下来了。所以真正有意义的不是平均速度，而是某一秒、某一个瞬间的速度是多少。数学家把这个问题写成极限，就得到了导数。而一旦我们把这个瞬时速度和极小的时间段结合起来，就有了“微分”。微分的意思是：在一个极小的时间间隔 dt 里，你走出去的那一小段路程叫做 ds，它等于速度乘以时间，也就是 ds = v(t)\,dt。你可以把整条路程想象成无数个微小的 ds 一点点拼出来的结果，就像一段流畅的动作其实由一帧帧画面连起来一样。微分做的事情，就是把这些“无限小的片段”刻画出来，让变化可以被追踪、被计算。

4、积分

说完了微分，我们自然就会遇到它的“孪生兄弟”——积分。微分是把一个过程拆开看，盯住那一瞬间的变化；积分则恰好相反，它是把无数个瞬间再拼接回去，重新得到整体。还记得刚才我们说的 ds = v(t)\,dt 吗？这玩意儿如果只看一瞬间，没啥意义，可一旦我们把所有时刻的 ds 都加起来，从 t=0 到 t=T，它就成了一段时间里的总路程：

这就是积分的本质：把“局部”拼成“整体”。想象你走路，每一步的快慢不一样，停顿、加速、减速交替出现，单看某一瞬间的速度你只知道当下，但只有把所有瞬间的变化都累积起来，你才知道最终走了多远。换句话说，积分就是帮你“结账”的那只算盘——你在时间轴上留下的每一笔运动痕迹，它都老老实实地加进去，最后告诉你一个总数。

生活里这事儿到处都是：水龙头滴水，每一秒滴几毫升，单看瞬间没啥，但积个一晚上，盆就满了；股票价格涨涨跌跌，每分钟的波动谁也说不清，可把面积加起来，你就能算出一整天的成交量。积分做的事，说白了就是“把细节还原成全貌”。

如果不笨的话，到此大家就应该知道极限、导数、微分、积分的基本概念了，剩下的怎么算其实都是相当工具化的数学方法论，这些数学方法并不比在工地上抡大锤复杂。

但到这里，很多人会觉得微积分似乎对我们没有任何用处，如果你有这种感觉，你觉得对其实也不对。

牛顿之所以被后人奉为大神，不光是因为他看苹果掉下来想到了万有引力，而是因为他手里有了微积分这把钥匙。你想想，如果只会代数，他能算出行星轨道吗？能描述出加速度、力和运动的关系吗？所以他干脆自己把微积分发明了出来，用它去刻画运动和力的连续变化。

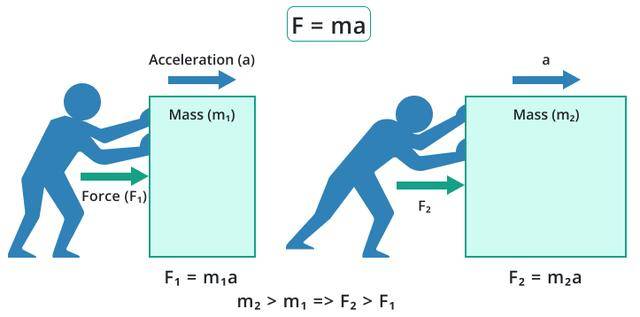
例如F = ma，这个公式怎么来的？其实就是牛顿用用微积分一路“算”出来！

在这个过程中，牛顿先观测冲量—动量关系：对物体作用一段时间的力，其“时间累积量”叫冲量。

量碰撞与拉压实验告诉我们：这个冲量正好等于动量变化 Δp。把极限放到瞬间，就得到连续形式

这一步已经把力学塞进了微积分：力是动量关于时间的导数。若质量恒定动量 p=mv，于是：

换句话说，力等于“速度的一阶导数再乘质量”，也等于“位置的二阶导数乘质量”。

在生活中F = ma大家耳熟能详的一个公式对吧，其实就是一个微积分计算之后的简化结果。

我们看到海面上的冰山就是“F = ma”，而它的微积分推导过程其实才是F = ma这个公式展开后的全貌。

大多数人觉得自己跟微积分没半点关系，说白了，是因为我们日常生活只碰到冰山露出水面的那一角——能用算术解决的问题已经绰绰有余了。买菜算钱、工资报表、手机分期，这些四则运算足够让日子过下去。可真要追问一句：这些计算的依据从哪儿来？这些事物背后有没有一套完整的数学模型？答案就指向了水下那片庞大的冰山——微积分。它并不高冷，相反，它就是那个能把零碎经验变成规律、把复杂现象抽丝剥茧的工具。但是，这个工具仅仅限于两种人接触，第一是真心喜欢数学和对数学感兴趣的人，第二就是类似于W君这样不得不用这些东西做工作中的工具的人。

只不过，真正用起来，掌握了使用方法你不会觉得微积分有多难。所以钱老说“人再笨，还能学不会微积分吗？”这话说得是完全正确的，钱老本人在数学界并不是牛顿、莱布尼茨、黎曼、希尔伯那种能在数学领域开天辟地的人物，他的水平——严格讲——也就是“用得熟”。他的厉害之处不在数学本身，而在于能把微积分这门工具玩得炉火纯青，用来解决空气动力学、控制论、航天工程中的实际问题。换句话说，钱老是个顶级“数学用户”，而不是数学的创造者。

当然了，前面还有粉丝回复要推荐几本数学书。W给出的推荐书单是：

没有数学基础的人（99%的普通人）先从《数学的故事》看起，看看你能不能喜欢上数学。

然后对数学有点兴趣之后去看《什么是数学》

这本书的唯一看点是——让你真正理解为什么数学不是“算数”这么简单。

然后，你就可以去看《微积分入门》这类的工具类使用书了。

看过这本书之后，你会觉得万物皆可微积分。

不过还得继续深入，你就应该看看《分析入门》或者叫做《Understanding Analysis （理解分析）》，Abbott的就没错了。

到这种书就已经进入真正的“学院派”了。看这本书会让一般仅仅是对数学感兴趣的人看起来非常痛苦。而且你越对数学感兴趣你就会越体会到这种痛苦。不过只要挺过来你会觉得自己在精神上脱胎换骨，原来你对极限、连续、导数、积分的理解会发生一次“彻底重构”：之前以为自己懂，其实只是“会用”；读完之后，你才知道什么叫“真正理解”。

不过，你以为这就能走出来了吗？还没呢，《分析入门》只是“入门”，还有更重要的是《数学分析原理》

很多人学到这里会“劝退”，因为这本书太干太硬了，但坚持下来的人，就会发现自己已经能独立地看懂学术论文、推导复杂模型了。基本上，你就能跟上韦神的课了。

到此基本上你也就不需要别人给你推荐书单了。如果真按照W君的建议做下去，W君心里冷笑一下，得嘞又送走一位……